A geometria fractal e os tubarões
Quando um tubarão avista ou sente o cheiro de um apetitoso pedaço de carne, ele não precisa de nenhuma geometria que o faça chegar até a comida; basta nadar até sua presa e então saborear o banquete. Mas o fato é que nem sempre o mar está para peixe ou, no caso do tubarão, para carnes. Nesses dias de falta de alimento, como é que ele se abastece?
Um artigo publicado na New Science apontou que alguns tubarões, quando não possuem presas a vista, seguem estratégias matemáticas para a caça. O artigo argumenta que tais tubarões se movem de forma sincronizada e padronizada, forma esta chamada por seus autores de “caminhada Levy” ou, matematicamente falando, geometria fractal.
Não há uma definição formal de fractal, visto que não há um termo ou uma linguagem matemática adequada. Grosso modo, um fractal é um objeto que pode ser dividido em partes, cada uma das quais semelhantes ao objeto original. Informalmente, podemos dizer que os fractais são semelhantes a irmãos gêmeos idênticos com personalidades diferentes.
Eles podem apresentar-se sob infinitas formas, não existindo uma aparência consensual. Contudo, há duas características muito frequentes em sua geometria: autossemelhança e complexidade infinita.
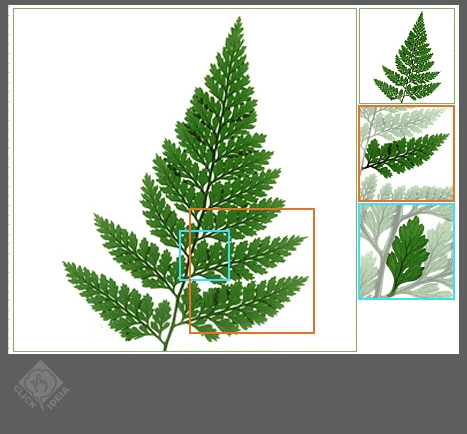
Tais conceitos são usados na arte, na ciência e na construção de tecnologias. Também podemos encontrá-los na natureza: samambaia, couve-flor, brócolis, árvores etc. No quadro ao lado você verá uma determinada árvore cuja parte está ampliada. Há semelhança com sua forma original em quaisquer dimensões que tomemos. Essa semelhança seria sempre a mesma, caracterizando um fractal.
Voltando aos tubarões, os pesquisadores descobriram esse fato rastreando tais animais durante 5700 dias e desenhando seu movimentos. Perceberam que havia uma padronização de movimentos infinitos, caracterizando a geometria fractal. A conclusão a que se chegou é que, por esse motivo, tais animais não evoluirão tanto quanto os demais nos últimos tempos.